Relazione (matematica)
Una relazione ( latino relatio "relazione", "relazione") è in genere un rapporto che può esistere tra le cose. Le relazioni in senso matematico sono esclusivamente quelle relazioni per le quali è sempre chiaro se esistono o meno; Gli oggetti non possono essere messi in relazione tra loro “in una certa misura”. Ciò consente una semplice definizione set- teorica del termine: una relazione è un insieme di tuple . Le cose che sono in relazione tra loro formano tuple, che sono elementi di .
Se non diversamente specificato, una relazione è generalmente intesa come una relazione a due cifre o binaria . In tale relazione, allora si formano due elementi e una coppia ordinata ha origine e da diversi livelli di base ed è il nome della relazione eterogenea o "relazione tra le quantità e ." Se le quantità di base corrispondono ( ), allora ciò significa la relazione omogeneamente o "Relazione nella o sulla folla ".
Casi speciali importanti, ad esempio relazioni di equivalenza e relazioni di ordine , sono relazioni su un insieme.
Oggi, alcuni autori considerano il termine relazione non necessariamente come quantità limitate a, ma lasciano che ciascuna classe costituita da coppie ordinate sia considerata relazione.
Definizioni
Relazione a due cifre
Una relazione a due cifre (chiamato anche relazione binaria ) tra due insiemi ed è un sottoinsieme del prodotto cartesiano
- .
L'insieme è indicato come l' insieme di origine (inglese: insieme di partenza ) della relazione , l'insieme come insieme di destinazione (inglese: insieme di destinazione ).
A volte, tuttavia, questa definizione non è abbastanza precisa e il riferimento alla quantità sorgente e target nella definizione di a, sopra è quindi un sottoinsieme del grafico (più raramente Count ) chiamato relazione. Una relazione a due cifre è quindi definita come una tripla
- con .
Conoscere l'insieme di origine e destinazione è particolarmente importante se le funzioni sono viste come relazioni speciali (cosiddette funzionali).
L' archetipo, argomento o definizione o pre-intervallo di una data relazione a due cifre è inteso come il più piccolo pre-intervallo possibile al grafico , i cui elementi compaiono tutti nelle coppie ordinate di effettivamente sul lato sinistro, nei segni
- .
L'intervallo di valori, valori o immagine o post-intervallo denota in questo senso il più piccolo post-intervallo per un dato , i cui elementi quindi compaiono tutti nelle coppie da destra, in caratteri
- .
Occasionalmente viene utilizzato il termine campo (o insieme di nodi ) per l' insieme di unione , in caratteri
- .
Inoltre, si possono trovare le seguenti designazioni:
- Dominio ( dominio inglese ) o per l'insieme di sorgenti (in linea di principio arbitrariamente grande) o per l'insieme di immagini originale (definito dal grafico) (dominio di definizione),
- Co-dominio ( codominio inglese , range ) sia per il set di destinazione che per il set di immagini,
- Insieme di nodi ( ) per il campo di una relazione.
Se due relazioni concordano nei loro grafici, si dice anche che sono essenzialmente uguali.
Esempio: ogni relazione è essenzialmente la stessa con e con la relazione omogenea .
relazione n -cifre
Più in generale, una relazione -digit è un sottoinsieme del prodotto cartesiano di insiemi
- con .
Qui denota la successione finita degli insiemi e il prodotto cartesiano.
La definizione più dettagliata può anche essere generalizzata alle relazioni -sign e si ottiene quindi la -tupla
- con .
Gli importi degli importi dei vettori caldi di relazione con il supporto minimo ammonta al grafico , vale a dire
- .
Il campo di una relazione a -cifre è dato da
- .
L'uguaglianza sostanziale è definita allo stesso modo delle relazioni a due cifre dalla corrispondenza dei grafici, in particolare ogni relazione a cifre è essenzialmente la stessa con e con la relazione omogenea .
- Relazione a una cifra e a zero cifre
Una relazione a una cifra su un insieme è quindi semplicemente un sottoinsieme , nella definizione dettagliata con .
Le relazioni a cifre zero sono quindi i sottoinsiemi del prodotto cartesiano vuoto o , cioè e , dettagliato e .
Relazioni tra o su classi reali
Spesso le aree portanti di una relazione non sono insiemi, ma vere e proprie classi , si parla quindi di relazioni di classe. Occasionalmente si possono evitare i problemi di teoria degli insiemi che ne derivano guardando solo il grafico della relazione corrispondente. Le quantità (minime) del vettore ( nel caso di definizione a due cifre e quantità di valore ) sono in realtà quantità, ma non è necessario specificare la quantità di origine , la quantità di destinazione , ... ( ) fin dall'inizio se le relazioni sono essenzialmente le stesso. Ciò non è sempre possibile, ad esempio per la relazione di equivalenza dell'uniformità , si veda anche: Numeri cardinali §Definizione . Essenzialmente l'uguaglianza dei rapporti è un altro esempio.
Una relazione di classe a due cifre con la classe di origine e la classe di destinazione è chiamata predecessore piccolo se la classe del predecessore (fibra archetipo di , vedi sotto) è un insieme (cioè non una classe reale) per tutti . La relazione si chiama inglese right-narrow (tedesco sul successore piccolo ), se per tutti la classe del successore (fibra immagine di ) è molto. Nel caso di giusta unicità (mappature parziali, mappature, vedi sotto), una relazione di classe è sempre piccola, poiché esiste un valore di immagine per ogni archetipo (esattamente o al massimo), cioè la classe dei successori è un insieme di quelli (o l' insieme vuoto ). Ogni mappatura delle classi iniettive è piccola e precedente piccola. La relazione di inclusione è piccola per ogni classe , poiché non possono essere classi reali, ma sono insiemi e quindi sono anche un insieme. I termini predecessore e successore stessi vengono solitamente utilizzati nel contesto delle relazioni d'ordine, vedere relazione d'ordine §Predecessori e successori .
Spiegazioni e annotazioni
Il prodotto cartesiano di due insiemi ed è l'insieme di tutte le coppie ordinate di e dove rappresenta ogni elemento dell'insieme e uno di . Nella coppia ordinata, l'ordine è importante; H. differisce da in contrasto con la coppia disordinata, che è identica a For , è scritto anche per far capire che c'è quella relazione tra gli oggetti (come in ). L' insieme vuoto come sottoinsieme del prodotto cartesiano inteso come relazione è chiamato relazione zero , il prodotto pieno è chiamato relazione tutto (chiamata anche relazione universale ) (indicata anche come ).
Relazioni e funzioni
- Una funzione è speciale, vale a dire una relazione univoca di sinistra totale e destra (a due cifre), vedere sotto per maggiori dettagli .
- Una multifunzione è una relazione totale sinistra .
- Una funzione parziale è una relazione non ambigua destra (generalmente non un totale sinistro) .
In tutti i casi (o se viene utilizzata la definizione dettagliata).
Quanto segue si applica alle funzioni e alle multifunzioni:
- Nella definizione più dettagliata , poiché è chiaramente definito da (totale sinistro), può anche essere omesso e utilizzato in modo più semplice .
Per le funzioni e le funzioni parziali vale quanto segue:
- For o è anche scritto (inglese: maplet ), or .
Generalmente:
- Le relazioni di luogo zero (come relazione zero-posto zero) e (come relazione zero-posto piena) hanno come funzioni caratteristiche le costanti booleane o logiche e , come sempre per relazione zero e tutte le relazioni.
- Il caso delle relazioni a una cifra è banale.
- Una relazione (o ) corrisponde in modo univoco a una funzione di verità . Questa funzione è anche nota come funzione indicatrice o funzione caratteristica del sottoinsieme (o ), dove può essere sostituita da .
- Una relazione a cifre (o ) corrisponde alla funzione caratteristica
Si applica quanto segue:
- .
- .
- .
- .
- Una relazione può essere intesa anche come mappatura di nell'insieme di potere di , si parla spesso di corrispondenza , e per di relazione di transizione .
Concatenamento di relazioni
Il concatenamento in avanti di due relazioni a due cifre è definito come segue:
Il concatenamento nell'ordine inverso è chiamato concatenamento all'indietro :
- .
Alcuni autori (W. v. O. Quine) usano la notazione per questo come alternativa .
La sequenza per il concatenamento all'indietro è la stessa delle funzioni di concatenamento (che possono essere viste come relazioni speciali).
La concatenazione di relazioni a due cifre è detta anche prodotto relativo . Nella concatenazione, il rapporto semplice che contenuto in ogni prodotto cartesiano può svuotare relazione ( insieme vuoto ) avviene, cioè, quando e disgiunti sono in simboli .
Esempio: la relazione “essere cognata di” è l'unione
- del prodotto relativo della relazione "essere fratello di" e della relazione "essere moglie di" e
- del prodotto relativo della relazione “essere sposa di” e della relazione “essere sorella di”.
relazione inversa
L' inversa relazione (chiamato anche converse relazione, converse o inversa relazione) è definita per un rapporto di due cifre come
- .
Occasionalmente, questo è indicato anche come relazione trasposta, in caratteri .
- Esempio 1: La relazione inversa della relazione "è discendente di" è la relazione "è antenato di".
- Esempio 2: La relazione inversa della relazione "è minore di" è la relazione "è maggiore di".
- Esempio 3: la relazione inversa della relazione "consegna a" è la relazione "è fornita da".
La generalizzazione della relazione inversa (conversa) alle relazioni -segno è la permutazione delle coordinate delle -tuple che contiene , speciale
- gli interscambi di sole 2 coordinate ( trasposizioni ) e
- l'inversione dell'ordine ( mirroring ),
entrambi esempi di permutazioni ( cicliche ) auto-inverse .
Sia una permutazione (cioè una mappatura biunivoca di su se stessa) e sia una relazione -place, quindi la relazione risultante dopo l'applicazione della permutazione è (si intende come una famiglia ). In caso di mirroring
è .
Immagine e archetipo
In una relazione a due cifre , l' immagine di un insieme o di una classe è l'insieme o la classe
- .
L' archetipo di un insieme o classe è l'insieme o classe
- .
Occasionalmente, si trova anche la designazione (sic!) per questo , spesso con parentesi quadre come annotato. In corrispondenza di a per la fibra immagine di un importo (Singleton) , la notazione è quella che utilizza in parte anche la notazione a parentesi in uso, i. H. ; nel caso di relazioni simmetriche, d. H. (eventualmente parziale) relazioni di equivalenza o compatibilità è la notazione e parla di classi di equivalenza o compatibilità o tolleranza.
Restrizione
Le relazioni possono essere limitate in modi diversi a sottoinsiemi degli insiemi di vettori, per maggiori dettagli vedere Limitazione di una relazione .
Relazione complementare
Per le relazioni a due cifre con un pre e post-intervallo fisso , la relazione complementare è data da
- ,
analogo per le relazioni a cifre per le aree di supporto fisse . Sui numeri reali , ad esempio, la relazione complementare a è .
Se si usa la notazione complessa , allora è
- ,
dove non ci sono più aggiunte esterne, ma componenti della relazione; analogo per le relazioni -digit in questa notazione.
Come per tutti gli insiemi, il complemento è involutivo anche per le relazioni:
- .
Relazioni omogenee
Se , allora, la relazione si dice omogenea. Alcuni autori definiscono una relazione generale già come una relazione omogenea, in quanto una relazione generale può sempre essere considerata come una limitazione omogenea: .
Relazioni omogenee speciali e operazioni su relazioni omogenee
Una speciale relazione omogenea in un insieme è la relazione di uguaglianza o identità o diagonale
Le notazioni alternative per la diagonale sono o ; se è già noto, viene semplicemente indicato come , o .
Un'altra relazione omogenea speciale è la relazione del tutto o relazione universale
- (indicato anche come Nabla come ).
Se è già noto, l'indice viene qui omesso, come nel caso della relazione di identità.
La relazione all gioca un ruolo nella teoria dei grafi (vedi sotto). Un esempio di utilizzo è la seguente frase:
- È un grafo diretto con molti angoli e una relazione (associata) di bordi, è quindi esattamente coerente (forte) quando la chiusura transitiva riflessiva della relazione universale.
La formazione della relazione inversa (relazione inversa) di una relazione omogenea a due cifre fornisce nuovamente una relazione omogenea a due cifre (vicinanza), l'esecuzione di due risultati di nuovo nella relazione iniziale (involutività). La connessione di una relazione arbitraria (anche non omogenea) con la relazione in cui viene convertita è simmetrica e riflessiva, cioè una relazione di equivalenza, ma in generale non è la stessa della relazione di identità.
Nel caso di una relazione omogenea , anche la concatenazione è una relazione omogenea, per cui le relazioni omogenee si formano in un monoide con la relazione moltiplicativa e l' elemento neutro . Così, e per generali poteri per definire, che è. è quindi anche chiamata la relazione unica sull'insieme .
In estensione della notazione invece che per la relazione inversa, si denotano le sue potenze con esponenti negativi:
- .
Qualsiasi numero intero è ammesso come esponente.
Inoltre, ogni monoide ha relazioni omogenee con la relazione vuota ( relazione zero )
un altro elemento assorbente .
I rapporti nascono dall'unione dei diversi poteri
- e .
Strutture algebriche
Prese insieme, le relazioni a due cifre su un insieme formano una relazione algebra
Usando le notazioni .
Insieme alle restrizioni, le relazioni omogenee formano un'algebra di Peirce ( eterogenea ) .
Relazioni omogenee a più cifre
Le relazioni omogenee a più cifre sono (con il loro grafico) sottoinsiemi di . Per solido la relazione di tutto (anche ) e la relazione di identità (diagonale) (anche ) sono date da
- .
L'applicazione delle permutazioni alle loro -uple, descritta come una generalizzazione della formazione delle conversioni, è qui di particolare importanza, poiché in questo modo si rimane sempre all'interno dei sottoinsiemi di (vicinanza). M. un. W. Queste operazioni sono mappature biunivoche in . Altri termini noti da relazioni a due cifre, come riflessività e simmetria, ecc., possono essere canonicamente (naturalmente) estesi a qualsiasi relazione a più cifre.
Teoria dei grafi e generalizzazioni
La teoria dei grafi descrive gli insiemi con una relazione con essi insieme ad alcune generalizzazioni sotto un termine generico comune, il grafico . I casi considerati nella teoria dei grafi sono (se non diversamente indicato) solitamente finiti.
1. Una struttura relazionale costituito da un complesso insieme con una relazione su di essa è chiamata diretta (anche orientata ) grafico . è chiamato l' insieme dei nodi del grafo, i suoi elementi sono chiamati nodi . è chiamato un sottoinsieme del gruppo di bordi , i suoi elementi (ordinate coppie ) sono chiamate dirette (cioè orientati ) bordi .
2. Grafici simmetrici , i. H. Gli insiemi con una relazione simmetrica sono equivalenti a un grafo non orientato il cui insieme di archi è costituito da archi ( non orientati ), vale a dire gli insiemi (disordinati) con (qui equivalente a ).
3. Ulteriori generalizzazioni riguardano i cosiddetti grafi orientati con archi multipli combinati , in cui ogni arco ha come molteplicità un numero naturale. I bordi di tali grafici possono essere rappresentati da un multiset : una mappa con un insieme e una mappa che assegna un numero positivo chiamato colore a ciascun nodo . I grafici con nodi e/o bordi colorati sono simili .
4. Di nodi e/o archi pesati : Parliamo di pesi anziché di colori se la mappatura è a valori reali. In Node Weighted questo corrisponde a un insieme fuzzy , in cui è un multiset a valori reali . Lo stesso vale per i bordi ponderati. Per i grafi orientati ciò significa in particolare che l'insieme degli archi (una relazione, cioè un insieme di coppie ordinate di nodi) diventa un insieme multiplo o fuzzy in un'estensione del concetto di relazione.
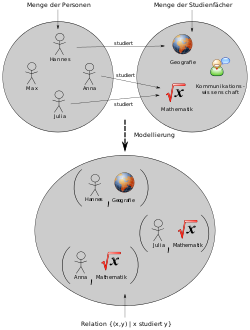
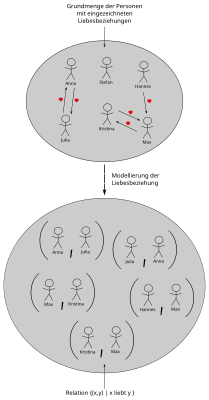
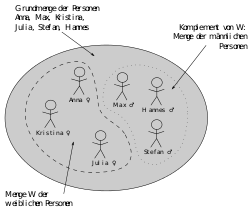
Esempi
Proprietà delle relazioni a due cifre
Relazioni generali
Le seguenti relazioni sono importanti per le funzioni (rappresentate come relazioni speciali). In generale, anche qui è possibile il rapporto tra due diverse quantità della causa .
| La relazione è chiamata | se e solo se (logica del predicato) | o equivalente (notazione di quantità) | e questo significa: |
|---|---|---|---|
|
sinistro totale o finale (multifunzione) |
Ogni elemento fuori ha almeno un partner dentro | ||
| diritto totale o suriettivo | Ogni elemento fuori ha almeno un partner dentro | ||
| lasciato inequivocabile o iniettivo | Ogni elemento da ha al massimo un partner in | ||
|
(legalmente) univoco (funzione parziale) |
Ogni elemento da ha al massimo un partner in |
| La relazione è chiamata | se e solo se (logica del predicato) | o equivalente (notazione di quantità) | e questo significa: |
|---|---|---|---|
| bittotale | Ogni articolo ha almeno un partner e viceversa. | ||
| inequivocabile | Ogni elemento out ha al massimo un partner in e viceversa. | ||
| biunivoco | Ogni elemento da ha esattamente un partner in | ||
| Figura o funzione | Ogni elemento da ha esattamente un partner in |
Funzioni
Panoramica delle proprietà funzionali per le relazioni
Una relazione è quindi una funzione (totale) se e solo se è lasciata totale e destra non ambigua. Ciò significa che ogni elemento in A ha esattamente un partner in B. Le proprietà suriettive, iniettive e biunivoche vengono solitamente utilizzate per le funzioni e specificano alcune proprietà aggiuntive. Ad esempio, una funzione (e qualsiasi relazione) è biunivoca se e solo se è suriettiva e iniettiva, cioè se la sua relazione inversa è una funzione.
| La relazione è chiamata | esattamente quando lei è a | è o equivalente (notazione di quantità) | e questo significa: |
|---|---|---|---|
| Suriezione | funzione suriettiva | Ogni elemento di ha esattamente un partner in e ogni elemento di ha almeno un partner in | |
| iniezione | funzione iniettiva | Ogni elemento di ha esattamente un partner in e ogni elemento di ha al massimo un partner in | |
| Biiezione | funzione biunivoca | Ogni elemento out ha esattamente un partner in e viceversa. |
Funzione inversa
Viene anche chiamata una mappatura o una funzione
- reversibile univoco o reversibile se biunivoco .
Una funzione è sempre reversibile come relazione, ma come funzione è reversibile proprio quando anche la sua relazione inversa è di nuovo una funzione, cioè quando di essa esiste una funzione inversa .
Relazioni omogenee
Gli esempi forniti nelle tabelle seguenti si riferiscono alla normale disposizione dei numeri reali quando si utilizza il segno di uguale “=”, il segno di minore o minore “<” e il segno di minore o uguale “≤”.
| La relazione è chiamata | se e solo se (logica del predicato) | o equivalente (notazione di quantità) | e questo significa: |
|---|---|---|---|
| comparativo destro o terzo uguale | Se due elementi sono correlati ciascuno allo stesso terzo elemento, allora sono anche correlati tra loro. Ad esempio, con e si applica sempre | ||
| comparativo sinistro o euclideo | Se un primo elemento è correlato a un secondo e un terzo elemento, anche questi sono correlati tra loro. Ad esempio, con ed è sempre lo stesso | ||
| transitivo | Se un primo elemento è relativo ad un secondo elemento e questo a sua volta è relativo ad un terzo elemento, anche il primo elemento è relativo al terzo elemento. Ad esempio, segue da e sempre | ||
| intransitivo | Se due elementi sono correlati e il secondo elemento è correlato a un terzo elemento, il primo elemento non è correlato al terzo elemento. Ad esempio, ogni numero naturale è il predecessore (immediato) di e il predecessore (immediato) di ma non è il predecessore (immediato) di |
La non transitività (cioè la relazione non è transitiva), l'intransitività e la transitività negativa sono diverse l'una dall'altra.
| La relazione è chiamata | se e solo se (logica del predicato) | o equivalente (notazione di quantità) | e questo significa: |
|---|---|---|---|
| riflessivo | Ogni elemento è correlato a se stesso, ad es. B. è sempre | ||
| irriflessivo | Nessun elemento è correlato a se stesso, ad es. B. non si applica a nessuno |
| La relazione è chiamata | se e solo se (logica del predicato) | o equivalente (notazione di quantità) | e questo significa: |
|---|---|---|---|
| simmetrico | La relazione è non orientata, ad es. B. segue sempre da (e viceversa) | ||
| antisimmetrico o identitario | Non ci sono due elementi diversi che sono correlati in entrambe le direzioni, ad es. B. segue da e sempre | ||
| asimmetrico | Non ci sono due elementi correlati in entrambe le direzioni, ad es. B. ne consegue sempre che non regge. |
| La relazione è chiamata | se e solo se (logica del predicato) | o equivalente (notazione di quantità) | e questo significa: |
|---|---|---|---|
| totale o completamente | Ogni due elementi sono correlati, ad es. B. se sempre o si applica. | ||
| konnex o connesso | Sono correlati due diversi elementi, ad es. B. se sempre o anche se sempre o si applica. | ||
| tricotomo | Ogni due elementi diversi sono sempre correlati esattamente in un modo, ad es. B. se o è sempre vero. |
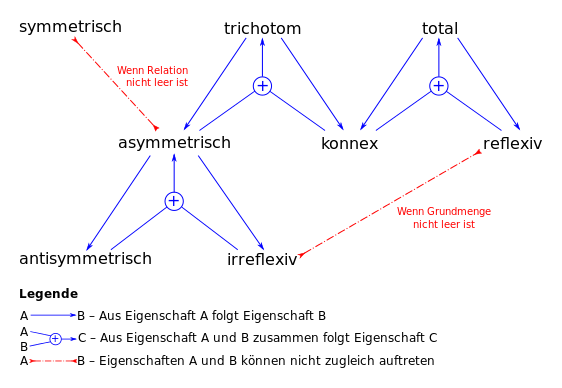
Le seguenti relazioni si applicano tra le proprietà:
Esistono le seguenti relazioni tra le proprietà di una relazione e quelle del suo complemento :
- è riflessivo è irriflessivo (e viceversa).
- è simmetrico è simmetrico.
- è antisimmetrico è connesso (e viceversa).
- è totale è asimmetrico (e viceversa).
Classi di relazioni
Altre importanti classi di relazioni e loro proprietà:
- Quasi-ordine o pre-ordine: transitivo e riflessivo
- Relazione di compatibilità orelazione di tolleranza : compatibile (riflessiva e simmetrica) (inglese: nella relazione di dipendenza al caso finito, nella relazione di tolleranza al caso transfinito).
- Relazione di equivalenza : transitiva, riflessiva e simmetrica
- Ordine parziale/ordine parziale , ordine parziale o ordine: transitivo, riflessivo e antisimmetrico.
- Ordine completo/ordine totale o ordine lineare: transitivo, riflessivo, antisimmetrico e totale
- Buon ordinamento : un ordine lineare in cui ogni sottoinsieme non vuoto di A, un elemento più piccolo ha
- Ordine rigoroso o rigoroso ordine parziale/ordine parziale: transitivo, irriflessivo e antisimmetrico (cioè asimmetrico)
- Ordine completo rigoroso/ordine totale o ordine rigoroso lineare: transitivo, irriflessivo, antisimmetrico e connesso
segno di relazione
Ci sono tre relazioni comparative di base in matematica elementare:
- (Esempio: "2 è inferiore a 3")
- (Esempio: "3 è uguale a 3")
- (Esempio: "3 è maggiore di 2")
con .
Due numeri reali hanno sempre esattamente una di queste relazioni tra loro. Con questi simboli di relazione se ne possono formare anche altri. Si applica quanto segue:
- , se o (esempio: "4 non è maggiore di 5")
- , se o (esempio: "5 non è inferiore a 5")
- , se o (esempio: "4 non è uguale a 5")
per tutti .
Le relazioni di ordine di cui sopra non esistono per i numeri complessi .
I matematici usano anche il segno ≤ per le relazioni d'ordine astratte (e ≥ per la relazione inversa associata) mentre “<” non è una relazione d'ordine nel senso della definizione matematica.
Per le relazioni di equivalenza si preferiscono simboli “simmetrici” come ≈, ~, ≡.
Teoria delle categorie
Per ogni semianello con elemento zero e un elemento , la seguente è una categoria :
- .
- Un morfismo è una funzione .
- Quanto segue si applica agli
oggetti
- .
- Questo è identico al delta di Kronecker : .
- Quanto segue si applica a
oggetti e morfismi
- .
I morfismi sono matrici set-indicizzate e la loro composizione avviene come per la moltiplicazione matriciale , corrisponde alla matrice unitaria .
In casi particolari , d. cioè, è la categoria delle relazioni.
utilizzo
Le operazioni su intere relazioni sono esaminate in algebra relazionale . In informatica , le relazioni sono importanti quando si lavora con i database relazionali .
Guarda anche
letteratura
- Garrett Birkhoff : Teoria del reticolo . 3. Edizione. AMS, Providence, RI 1973, ISBN 0-8218-1025-1 .
- Stefan Brass: logica matematica con applicazioni di database . Martin Luther University Halle-Wittenberg, Institute for Computer Science, Halle 2005, p. 176 ( informatik.uni-halle.de [PDF]).
- Marcel Erné: Introduzione alla teoria dell'ordine . Bibliographisches Institut, Mannheim 1982, ISBN 3-411-01638-8 .
- Helmuth Gericke: Teoria delle associazioni . Istituto bibliografico, Mannheim 1963.
- Dieter Klaua : teoria degli insiemi . De Gruyter, Berlino / New York 1979, ISBN 3-11-007726-4 (L'autore usa il termine corrispondenza in senso insiemistico come sinonimo di relazione, ma poi usa il simbolo al posto di . Nell'articolo qui, invece, o (grafico di ) scritto).
- H. König: Progettazione e teoria strutturale dei controlli per gli impianti di produzione (= ISW Research and Practice . Volume 13 ). Springer, Berlino / Heidelberg 1976, ISBN 3-540-07669-7 , pp. 15-17 , doi : 10.1007 / 978-3-642-81027-5_1 .
- Ingmar Lehmann , Wolfgang Schulz: Insiemi - Relazioni - Funzioni . Una chiara introduzione. 3a edizione riveduta e ampliata. Vieweg + Teubner, Wiesbaden 2007, ISBN 978-3-8351-0162-3 .
- Heike Mildenberger: Teoria degli insiemi assiomatica . Università di Friburgo, 9 novembre 2015, p. 58 ( mathematik.uni-freiburg.de [PDF]).
- Willard van Orman Quine : Teoria degli insiemi e sua logica (= logica e fondamenti della matematica . Volume 10 ). Vieweg + Teubner, Wiesbaden 1973, ISBN 3-528-08294-1 , pp. 264 (Inglese americano: Teoria degli insiemi e sua logica . Cambridge, MA 1963. Brossura Ullstein 1978).
- Gerard O'Regan: Guida alla matematica discreta. Insiemi, Relazioni e Funzioni (= Testi in Informatica (TCS) ). Springer, Svizzera 2016, p. 25–51 , doi : 10.1007 / 978-3-319-44561-8_2 ( springer.com [PDF; 1000 kB ]).
- Fritz Reinhardt, Heinrich Soeder: dtv atlas matematica . 11a edizione. nastro 1 : Fondamenti, Algebra e Geometria. Deutscher Taschenbuchverlag, Monaco di Baviera 1998, ISBN 3-423-03007-0 , p. 30-33, 42-45 .
- Gunther Schmidt, Thomas Ströhlein: Relazioni e grafici . Springer, Berlino et al. 1989, ISBN 3-540-50304-8 .
- Robert Wall: Introduzione alla logica e alla matematica per i linguisti . nastro 1 : Logica e teoria degli insiemi . Bibliotecario, Kronberg / Ts. 1974, ISBN 3-589-00023-6 .
- Siegfried Wendt: Fondamenti non fisici dei formalismi interpretati dalla tecnologia dell'informazione . 2a edizione. Springer, Berlino / Heidelberg 2013, ISBN 978-3-540-54452-4 , doi : 10.1007 / 978-3-642-87627-1 ( libri.google.de ).
link internet
- Letteratura sulla relazione nel catalogo della Biblioteca nazionale tedesca
- Video: idea delle relazioni a due cifre . University of Education Heidelberg (PHHD) 2012, messa a disposizione dalla Technical Information Library (TIB), doi : 10.5446 / 19788 .
Riferimenti e commenti individuali
- ↑ a b G. Smolka: Programmazione: Capitolo 2 - Teoria degli insiemi , presso: Saarland University, 20 maggio 2003, § 2.5. Relazioni binarie, pagina 15.
- ^ Walter Gellert, Herbert Kästner , Siegfried Neuber (a cura di): Lexicon of Mathematics. Bibliographisches Institut Lipsia, 1979, pagina 484.
- ↑ a b Albert Monjallon: introduzione alla matematica moderna. Edizione 2. Springer-Verlag, 2013, ISBN 978-3-663-16043-4 , pagina 74. doi: 10.1007 / 978-3-663-16043-4 , (books.google.de)
- ↑ a b Wilhelm Dangelmaier: Teoria della produzione 1: Fondamenti metodici . Springer-Verlag, 2017, ISBN 978-3-662-54922-3 , pagina 478. doi: 10.1007 / 978-3-662-54923-0 (books.google.de)
- ↑ a b Cobocard: pre-area e post-area.
- ↑ a b Matheboard: Relazioni: cosa si intende esattamente per intervallo pre/post di una relazione?
- ↑ Dieter Klaua: Teoria degli insiemi . Pagina 62, definizione 5 (1a parte).
- ↑ a b c H. König: Teoria della progettazione e della struttura dei controlli per gli impianti di produzione. Pagina 19.
-
↑ Ulteriori notazioni:, nella letteratura in lingua inglese :, vedere: Gerard O'Regan: Sets, Relations and Functions. pag. 36.
- ↑ Dieter Klaua: Teoria degli insiemi . Pagina 62, definizione 5, (seconda parte).
-
↑ Ulteriori notazioni:, nella letteratura in lingua inglese
:, vedere: Gerard O'Regan: Sets, Relations and Functions. pag. 36.
- ↑ Dieter Klaua: Teoria degli insiemi . Pagina 62, definizione 5, (terza parte).
- ↑ Nella teoria delle strutture algebriche , soprattutto per quanto riguarda la teoria delle categorie, i termini dominio e codominio sono usati per lo più nel senso di insiemi sorgente e target, mentre negli scritti introduttivi alla teoria degli insiemi questi sono solitamente definiti come archetipo e insiemi di immagini,
- ↑ anche quantità simile , modo quantitativo , per ger. Sinistra stretto o set-like chiamato, vedi Wikibooks: Mathematics Glossario: attributi teorico: piccolo predecessore
- ↑ Heike Mildenberger 2015, p.59f.
- ↑ Martin Ziegler: Lezione sulla teoria degli insiemi , Università di Friburgo, 1992–2014, pagina 12.
- ↑ Azriel Levy: Teoria degli insiemi di base (= Dover Books on Mathematics . Volume 13). Courier Corporation, Newburyport 2012, ISBN 978-0-486-15073-4 , pagina 22, (in linea)
- ↑ Se elementi primitivi sono consentiti: per gli elementi primitivi si è anche un set.
- ↑ Vedi anche: Teoria degli insiemi assiomatici, Ottenere un modello di (ZF - Fnd) ∪ {¬Fnd} da un modello di ZF , Ben Gurion University (BGU) del Negev, The Department of Mathematics, 2003.
- ↑ Nel caso generale con la sequenza dell'importo del sostegno è la Allrelation , nel caso omogeneo, con le n volte l'importo del sostegno è .
- ↑ Stefan Brass (2005), pagina 19.
- ↑ La funzione caratteristica come funzione di verità corrisponde quindi a un predicato logico , e nella teoria dei modelli i simboli di relazione sono quindi anche chiamati simboli di predicato, vedi Stefan Brass (2005) p.16.
- ↑ Inglese: composizione relazionale in avanti
- ^ Scambio di stack di matematica: composizione in avanti e all'indietro nell'algebra relazionale Discussione sulle direzioni di concatenamento in relazione al concatenamento di funzioni come relazioni speciali. La notazione Maplet viene talvolta utilizzata per le coppie ordinate :
- ↑ a b c Glossario della notazione Z §Relazioni , Università di Washington
-
↑ Occasionalmente è presente anche il punto e virgola nella rappresentazione dei contorni. Tuttavia, a seconda dell'hardware e delle impostazioni, non viene sempre visualizzato correttamente in Wikipedia.
- ↑ Inglese: composizione relazionale a ritroso
- ↑ a b H. König: Teoria della progettazione e della struttura dei controlli per gli impianti di produzione. Pagina 21.
- ↑ un b c W. v. O. Quine: Teoria degli insiemi e sua logica. Pagina 47.
- ^ Algebra relazionale. In: Mathepedia.de.
- ↑ Notato anche come biiezione .
- ↑ Per la notazione, vedere Gary Hardegree: Teoria degli insiemi, Capitolo 2: Relazioni , Università del Massachusetts, Amherst, Dipartimento di Filosofia, Autunno 2015, pagina 11: D16 e D17. Contrariamente alle altre notazioni, questi simboli fanno riferimento a immagini (funzioni) tra gli insiemi di potenza .
- ↑ Analogo a: D. Klaua: Teoria degli insiemi . P. 63, definizione 6 (a).
- ↑ Nel caso delle relazioni d'ordine e simili, alcuni autori parlano anche di un insieme o di una classe predecessore, vedi Heike Mildenberger 2015, p.6, definizione 1.12.
- ↑ W. v. O. Quine: Teoria degli insiemi e sua logica. Pagina 17. Attenzione: la stampa è intitolata come immagine , ma definisce chiaramente l' immagine originale (un insieme di coordinate di sinistra = argomenti ). Si noti che questa notazione è usata al contrario delle funzioni qui; per le funzioni sta per l' immagine (un insieme di coordinate della mano destra = valori di funzione ) di un insieme sotto una funzione . Le funzioni sono relazioni speciali. Vedi immagine (matematica) §Notazioni alternative .
- ↑ Johannes Köbler: Introduzione all'informatica teorica: relazioni. Università Humboldt di Berlino, Istituto di informatica WS2013 / 14, pagina 68.
- ↑ W. v. O. Quine: Teoria degli insiemi e sua logica. Pagina 17.
- ↑ Seguendo la definizione dettagliata della relazione sopra, si comprenderà la diagonale come il grafico dell'identità: (Relazione) con (Grafico).
- ↑ Seguendo la definizione di relazione dettagliata di cui sopra si comprenderà il Nabla come il grafico di tutte le relazioni in analogia alla diagonale: (Relazione) con (Grafico)
- ↑ Questo può portare a confusione con il prodotto cartesiano con piombo. Il significato risulta in ogni caso dal contesto.
- ^ A B Gerard O'Regan: Insiemi, relazioni e funzioni. pag. 39.
- ↑ Vedi anche: Kleenesche busta .
- ↑ Per le proprietà di transitività di queste associazioni, vedere Dimostrare che è una relazione transitiva su A , su: StackExchange: Mathematics 2018.
- ↑ Robin Hirsch, Ian Hodkinson: Algebre relazionali. P. 7, su: Terza Conferenza indiana sulla logica e le sue applicazioni (ICLA). 7-11 Gennaio 2009, Chennai, India.
- ↑ Dei link (a una cifra) e (a due cifre) - in senso stretto - si intendono le restrizioni su o .
- ^ C. Brink, K. Britz, RA Schmidt: Algebre di Peirce. (1994), pp.163f. In: M. Nivat, C. Rattray, T. Rus, G. Scollo (a cura di): Metodologia algebrica e tecnologia del software (AMAST'93). Laboratori di informatica. Springer, Londra.
- ↑ Il termine grafico nel senso grafico-teorica deve essere distinto dal termine grafico di un rapporto secondo la definizione dettagliata dei rapporti citati all'inizio (così come le immagini), che non viene utilizzato nella teoria dei grafi.
-
↑ Il colore termine deriva dal fatto che il numero intesa come molteplicità secondo la teoria multimetary viene riprodotto nella rappresentazione visiva come colore numero codificato del bordo , analogamente a nodi colorati . Un esempio di numeri di colore sarebbero i colori RAL .
- ↑ WD Blizard: Multiset a valori reali e Fuzzy Set. In: Insiemi e sistemi fuzzy. Vol. 33, 1989, pp. 77-97. doi: 10.1016 / 0165-0114 (89) 90218-2 .
-
↑ "Due quantità uguali a uno e lo stesso terzo sono uguali tra loro" Cfr.
Henri Poincaré: Wissenschaft und Hypothese. Autore. Edizione tedesca con est. Nota da F. e L. Lindemann. Teubner, Lipsia 1904, pagina 36. - ↑ Wolfgang Rautenberg: Introduzione alla logica matematica. Un libro di testo. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8348-0578-2 , pagina 42.
- ↑ Il 1° assioma negli Elementi di Euclide può, d'altra parte, essere visto anche come equivalente al terzo uguale .
- ↑ Non è raro che konnex sia definito come totale .
- ↑ Questo è facile da vedere dalle tabelle sopra (1a e 2a colonna) tenendo conto , i. H. e le regole della logica dei predicati. Le inversioni si applicano a causa dell'involutività .
- ↑ Wendt 2013, pagina 31



















































































































![{\ stile di visualizzazione R [Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9ca7f0a1fdfe689def5adb90032f7da6c9ffc93)


![{\ stile di visualizzazione R [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33ac134e157437a3986ad725151bf8e5fe566156)
![{\ displaystyle [a] _ {R} = R \ langle \ {a \} \ rangle = R ^ {- 1} \ langle \ {a \} \ rangle}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc947079ddacce3198f75fca059a2f3ad5e4332)




























































![{\ displaystyle f \ due punti \; M \ a [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/981c1ffde3d83759978efcfb0871056111d361cd)