Distribuzione binomiale negativa

Distribuzione binomiale negativa
Distribuzione di probabilità distribuzione di probabilità di variante B . In questo esempio, parametro di una funzione, in modo che si applica (che richiede ). Il valore atteso viene visualizzato come una linea arancione; la deviazione standard come verde. ${\ displaystyle p}$${\ displaystyle r}$${\ displaystyle E [X] = 10}$${\ displaystyle p = r / (r + 10)}$
Funzione di distribuzione
parametro	r > 0 - numero di successi fino al termine p ∈ (0,1) - probabilità di successo singolo
vettore	k ∈ {0, 1, 2, 3,…} - numero di errori
Funzione di probabilità	${\ displaystyle {k + r-1 \ scegli k} \ cdot p ^ {r} (1-p) ^ {k}}$
Funzione di distribuzione	${\ displaystyle 1-I_ {1-p} (k + 1, \, r)}$ Funzione beta di Eulero
Valore atteso	${\ displaystyle {\ frac {r (1-p)} {p}}}$
modalità	${\ displaystyle \ left \ lfloor {\ frac {(1-p) (r-1)} {p}} \ right \ rfloor}$
Varianza	${\ displaystyle {\ frac {r (1-p)} {p ^ {2}}}}$
Disonestà	${\ displaystyle {\ frac {2-p} {\ sqrt {r (1-p)}}}}$
Rigonfiamento	${\ displaystyle {\ frac {6} {r}} + {\ frac {p ^ {2}} {r (1-p)}}}$
Funzione generatrice di momenti	${\ displaystyle \ left ({\ frac {pe ^ {s}} {1- (1-p) e ^ {s}}} \ right) ^ {r} \! \! \!, s <| \ ln (1-p) |}$
Funzione caratteristica	${\ displaystyle \ left ({\ frac {pe ^ {\ mathrm {i} s}} {1- (1-p) e ^ {\ mathrm {i} s}}} \ right) ^ {r}}$

La distribuzione binomiale negativa (chiamata anche distribuzione Pascal ) è una distribuzione di probabilità univariata . È una delle distribuzioni di probabilità discrete ed è una delle tre distribuzioni di Panjer .

Descrive il numero di tentativi necessari per ottenere un dato numero di successi in un processo Bernoulli .

Oltre alla distribuzione di Poisson , la distribuzione binomiale negativa è la più importante distribuzione del numero di perdite nella matematica attuariale . Qui viene utilizzato in particolare per distribuire il numero di sinistri nell'assicurazione sanitaria, meno spesso nel settore della responsabilità civile automobilistica o dell'assicurazione globale.

Derivazione della distribuzione binomiale negativa

Funzione di probabilità della distribuzione binomiale negativa (variante A) per ; (blu), (verde) e (rosso)${\ displaystyle r = 10}$${\ displaystyle p = 0.2}$${\ displaystyle p = 0,5}$${\ displaystyle p = 0,8}$

Con l'aiuto del modello dell'urna , questa distribuzione può essere descritta come rimessa: in un'urna ci sono due tipi di palline ( popolazione dicotomica ). La proporzione delle palline del primo tipo è . La probabilità che venga tirata una palla di prima elementare è quindi pari . ${\ displaystyle p}$${\ displaystyle p}$

Una palla viene ora estratta e rimessa a posto finché il primo tipo di palle non è esattamente del primo tipo. È possibile definire una variabile casuale : "Numero di tentativi per ottenere il successo per la prima volta ". Il numero di tentativi è nell'ammontare . numerabilmente ha un numero infinito di possibili manifestazioni. ${\ displaystyle r}$ ${\ displaystyle X}$${\ displaystyle r}$${\ displaystyle \ {n \ in \ mathbb {N} | n \ geq r \}}$${\ displaystyle X}$

La probabilità che siano stati necessari tentativi per raggiungere il successo viene calcolata in base alla seguente considerazione: ${\ displaystyle n}$${\ displaystyle r}$${\ displaystyle P (X = n)}$

A questo punto dovrebbero essere già stati effettuati tentativi. Sono state estratte in totale palline del primo tipo. La probabilità di ciò è data dalla distribuzione binomiale delle variabili casuali : "Numero di palline del primo tipo negli esperimenti": ${\ displaystyle n-1}$${\ displaystyle r-1}$${\ displaystyle Y}$${\ displaystyle n-1}$

${\ Displaystyle \ operatorname {P} (Y = r-1) = {{n-1} \ scegli {r-1}} p ^ {r-1} (1-p) ^ {n-1- (r -1)}.}$

La probabilità che ora venga estratta un'altra palla del primo tipo è allora

${\ Displaystyle \ operatorname {P} (X = n) = \ operatorname {P} (Y = r-1) \ cdot p.}$

Una variabile casuale è chiamata distribuzione binomiale negativa con i parametri (numero di tentativi riusciti) e (probabilità di occorrenza di un successo in un singolo tentativo ), se ad essa si applica la funzione di probabilità${\ displaystyle X}$ ${\ Displaystyle \ operatorname {NB} (r, p)}$${\ displaystyle r}$${\ displaystyle p}$

${\ Displaystyle \ operatorname {P} (X = n) = {{n-1} \ scegli {r-1}} p ^ {r} (1-p) ^ {nr}}$

consente di specificare.

Questa variante è chiamata variante A qui per evitare confusione.

Definizione alternativa

Una variabile casuale discreta è soggetta alla distribuzione binomiale negativa con i parametri e , se sono le probabilità ${\ displaystyle X}$${\ Displaystyle \ operatorname {NB} (r, p)}$${\ displaystyle r}$${\ displaystyle p}$

${\ Displaystyle \ operatorname {P} (X = k) = {k + r-1 \ scegli k} p ^ {r} (1-p) ^ {k} = {{k + r-1} \ scegli k } p ^ {r} q ^ {k} = {{- r} \ scegli k} p ^ {r} (- q) ^ {k}}$

per i propri. ${\ displaystyle k = 0,1,2 \ dotsc}$

Entrambe le definizioni sono correlate sopra ; Mentre la prima definizione chiede il numero di tentativi (riusciti e non riusciti) fino a quando non si verifica il -esimo successo, la rappresentazione alternativa è interessata al numero di fallimenti fino a quando non si verifica il -esimo successo. I successi non vengono conteggiati. La variabile casuale descrive quindi solo il numero di tentativi falliti. ${\ displaystyle n = k + r}$${\ displaystyle n}$${\ displaystyle r}$${\ displaystyle k}$${\ displaystyle r}$${\ displaystyle r}$${\ displaystyle X}$

Questa variante è chiamata variante B qui .

Proprietà della distribuzione binomiale negativa

Valore atteso

opzione A

Il valore atteso è determinato ad essere

${\ Displaystyle \ operatorname {E} (X) = {\ frac {r} {p}} \,}$.

Variante B

Con la definizione alternativa, il valore atteso è minore, ad es. ${\ displaystyle r}$

${\ displaystyle \ operatorname {E} (X) = {\ frac {r} {p}} - r = {\ frac {r (1-p)} {p}}}$.

Varianza

La varianza della distribuzione binomiale negativa è data da per entrambe le definizioni

${\ Displaystyle \ operatorname {Var} (X) = {\ frac {r (1-p)} {p ^ {2}}}}$.

Con la definizione alternativa, la varianza è sempre maggiore del valore atteso (sovra- dispersione ).

Coefficiente di variazione

opzione A

Di aspettativa e varianza, risulta immediatamente il coefficiente di variazione a

${\ displaystyle \ operatorname {VarK} (X) = {\ sqrt {\ frac {1-p} {r}}}}$

Variante B

Nella rappresentazione alternativa il risultato è

${\ Displaystyle \ operatorname {VarK} (X) = {\ frac {1} {\ sqrt {r (1-p)}}}}$.

Disonestà

L' inclinazione risulta per entrambe le varianti come segue:

${\ Displaystyle \ operatorname {v} (X) = {\ frac {2-p} {\ sqrt {r (1-p)}}}}$.

Rigonfiamento

L'eccesso è per entrambe le varianti

${\ displaystyle \ gamma = {\ frac {6} {r}} + {\ frac {p ^ {2}} {r (1-p)}}}$.

Quindi questo è il rigonfiamento

${\ displaystyle \ beta _ {2} = {\ frac {6} {r}} + {\ frac {p ^ {2}} {r (1-p)}} + 3}$.

Funzione caratteristica

opzione A

La funzione caratteristica ha la forma

${\ displaystyle \ varphi _ {X} (s) = \ left ({\ frac {pe ^ {\ mathrm {i} s}} {1- (1-p) e ^ {\ mathrm {i} s}} } \ right) ^ {r}}$.

Variante B

In alternativa si presenta

${\ displaystyle \ varphi _ {X} (s) = \ left ({\ frac {p} {1- (1-p) e ^ {is}}} \ right) ^ {r}}$.

Funzione generatrice di probabilità

opzione A

Per la funzione generatrice di probabilità si ottiene

${\ displaystyle m_ {X} (s) = \ left ({\ frac {ps} {1- (1-p) s}} \ right) ^ {r}}$con .${\ displaystyle 0 <s <{\ frac {1} {1-p}}}$

Variante B

L'analogico è quindi

${\ displaystyle m_ {X} (s) = \ left ({\ frac {p} {1- (1-p) s}} \ right) ^ {r}}$.

Funzione generatrice di momenti

opzione A

La funzione generatrice del momento della distribuzione binomiale negativa è

${\ displaystyle M_ {X} (s) = \ left ({\ frac {pe ^ {s}} {1- (1-p) e ^ {s}}} \ right) ^ {r}}$con .${\ displaystyle s <| \ ln (1-p) |}$

Variante B

Poi c'è il display alternativo

${\ displaystyle M_ {X} (s) = \ left ({\ frac {p} {1- (1-p) e ^ {s}}} \ right) ^ {r}}$

Somma di variabili casuali binomiali negative

Sono due variabili casuali binomiali negative indipendenti per i parametri e . Quindi c'è di nuovo una distribuzione binomiale negativa per il parametro e . La distribuzione binomiale negativa è quindi riproduttiva , per la convoluzione essa sostiene che ${\ displaystyle X_ {1}, X_ {2}}$${\ displaystyle r_ {1}, r_ {2}}$${\ displaystyle p}$${\ displaystyle X_ {1} + X_ {2}}$${\ displaystyle r_ {1} + r_ {2}}$${\ displaystyle p}$${\ Displaystyle \ operatorname {NB} (r_ {1}, p) * \ operatorname {NB} (r_ {2}, p) = \ operatorname {NB} (r_ {1} + r_ {2}, p)}$

forma un semigruppo di convoluzione .

Generalizzazione a parametri reali

La derivazione e l'interpretazione di cui sopra della distribuzione binomiale negativa utilizzando il modello urna è possibile solo per. Tuttavia, esiste anche una generalizzazione della distribuzione binomiale negativa per . A tal fine si considera una distribuzione di Poisson la cui intensità è distribuita casualmente secondo una distribuzione gamma con i parametri e . Se ora si forma la distribuzione mista di queste due distribuzioni, si ottiene la cosiddetta distribuzione di Poisson-gamma . Quanto segue si applica quindi alla funzione di probabilità di questa distribuzione ${\ displaystyle r \ in \ mathbb {N}}$${\ displaystyle r \ in \ mathbb {R} ^ {+}}$ ${\ displaystyle P (k | \ lambda)}$${\ displaystyle \ lambda}$${\ displaystyle r}$${\ displaystyle {\ frac {p} {1-p}}}$

${\ displaystyle {\ begin {align} f (k | r, p) & = \ int _ {0} ^ {\ infty} f _ {\ text {Poi}} (k | \ lambda) \ cdot f _ { \ text {Gamma}} (\ lambda | r, {\ frac {p} {1-p}}) \; \ mathrm {d} \ lambda \\ [8pt] & = \ int _ {0} ^ {\ infty} {\ frac {\ lambda ^ {k}} {k!}} e ^ {- \ lambda} \ cdot \ lambda ^ {r-1} {\ frac {e ^ {- \ lambda p / (1- p)}} {{\ big (} {\ frac {1-p} {p}} {\ big)} ^ {r} \, \ Gamma (r)}} \; \ mathrm {d} \ lambda \ \ [8pt] & = {\ frac {p ^ {r} (1-p) ^ {- r}} {k! \, \ Gamma (r)}} \ int _ {0} ^ {\ infty} \ lambda ^ {r + k-1} e ^ {- \ lambda / (1-p)} \; \ mathrm {d} \ lambda \\ [8pt] & = {\ frac {(p) ^ {r} ( 1- p) ^ {- r}} {k! \, \ Gamma (r)}} \ (1-p) ^ {r + k} \, \ Gamma (r + k) \\ [8pt] & = {\ frac {\ Gamma (r + k)} {k! \; \ Gamma (r)}} \; (1-p) ^ {k} p ^ {r}. \ end {allineato}}}$

Poiché otteniamo la funzione di probabilità della distribuzione binomiale negativa. Pertanto, anche la distribuzione binomiale negativa può essere interpretata come significativa. La probabilità di raggiungere il successo è quindi uguale alla probabilità di ottenere il successo con una distribuzione binomiale con parametri casuali e gamma-distribuiti . Le funzioni gamma nella funzione di probabilità possono anche essere sostituite da coefficienti binomiali generalizzati. ${\ displaystyle r \ in \ mathbb {N}}$${\ displaystyle r \ in \ mathbb {R} ^ {+}}$${\ displaystyle k}$${\ displaystyle k}$

Questa costruzione corrisponde alla variante B definita sopra.Tutte le caratteristiche, come il valore atteso, la varianza e così via, rimangono invariate. Inoltre, la variante reale è divisibile all'infinito . ${\ displaystyle r> 0}$

Rapporti con altre distribuzioni

Relazione con la distribuzione geometrica

La distribuzione binomiale negativa passa alla distribuzione geometrica . D'altra parte, la somma di variabili casuali distribuite geometricamente reciprocamente indipendenti con lo stesso parametro è distribuita in modo binomiale negativamente con i parametri e . Tuttavia, è necessario notare anche qui quale variante di parametrizzazione è stata selezionata. Essendo la somma di variabili casuali indipendenti e identicamente distribuite, la distribuzione per quelle grandi è approssimativamente normale. ${\ displaystyle r = 1}$${\ displaystyle X = \ sum _ {i = 1} ^ {r} X_ {i}}$${\ displaystyle X_ {1}, \ dots, X_ {r}}$${\ displaystyle p}$${\ Displaystyle \ operatorname {NB} (r, p)}$${\ displaystyle p}$${\ displaystyle r}$${\ displaystyle X}$${\ displaystyle r}$

Relazione con la distribuzione di Poisson composta

La distribuzione binomiale negativa deriva dalla distribuzione composita di Poisson quando combinata con la distribuzione logaritmica . I parametri vanno alla variante B con e . ${\ displaystyle p _ {\ text {log}} = 1-p _ {\ text {neg}}}$${\ displaystyle \ textstyle r = {\ frac {- \ lambda} {\ ln (1-p _ {\ text {log}})}}}$

esempio

Funzione di probabilità della distribuzione binomiale negativa

Funzione di distribuzione della distribuzione binomiale negativa

La studentessa Paula sta giocando a skat stasera. Sa per lunga esperienza che vince ogni quinta partita. La vittoria è definita come segue: devi prima ottenere una partita facendo un'offerta, poi devi vincere questa partita.

Dato che domani alle otto terrà una lezione di statistica, la serata non dovrebbe essere troppo lunga. Ecco perché ha deciso di tornare a casa dopo aver vinto la decima partita. Supponiamo che un gioco duri circa 4 minuti (generosamente calcolato). Qual è la probabilità che possa tornare a casa dopo due ore, cioè dopo 30 partite?

Procediamo con le nostre considerazioni come sopra:

Qual è la probabilità che abbia vinto 9 volte in 29 partite? Calcoliamo questa probabilità con la distribuzione binomiale, secondo il modello dell'urna con 29 tentativi e 9 palline del primo tipo:

${\ displaystyle P (Y = 9) = {29 \ scegli 9} 0 {,} 2 ^ {9} \ cdot 0 {,} 8 ^ {20} = 0 {,} 0591.}$

La probabilità di ottenere la decima vittoria alla 30esima partita è ora

${\ displaystyle P (X = 30) = 0 {,} 0591 \ cdot 0 {,} 2 = 0 {,} 0118.}$

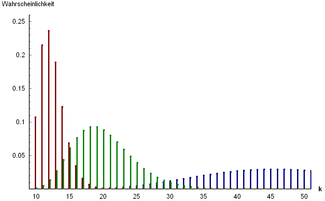
Questa probabilità ora sembra essere molto piccola. Il grafico della variabile casuale binomiale negativa X mostra che nel complesso le probabilità rimangono molto piccole. Come potrà mai andare a letto la povera Paula? Possiamo tranquillizzarla: basta chiedere quanti tentativi ha bisogno al massimo Paula , non devono essere esattamente 30.

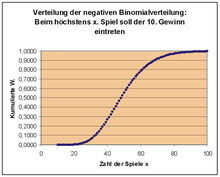
La probabilità che siano necessari al massimo 30 tentativi è la funzione di distribuzione F (x) della distribuzione binomiale negativa in x = 30, che qui è la somma delle probabilità P (X = 0) + P (X = 1) + Risultati P (X = 2) + ... + P (X = 30). Uno sguardo al grafico della funzione di distribuzione mostra: se Paula è soddisfatta con una probabilità del 50%, dovrebbe giocare al massimo circa 50 partite, ovvero 50,4 min = 200 min = 3 h 20 min. 80% di probabilità Per ottenere le sue 10 vincite, dovrebbe giocare al massimo circa 70 partite, cioè poco meno di 5 ore. Forse Paula dovrebbe cambiare la sua strategia sui numeri di gioco, dopotutto.

link internet

• AV Prokhorov: distribuzione binomiale negativa . In: Michiel Hazewinkel (a cura di): Encyclopedia of Mathematics . Springer-Verlag e EMS Press, Berlino 2002, ISBN 978-1-55608-010-4 (inglese, online ). 
• Eric W. Weisstein : Negative Binomial Distribution . In: MathWorld (inglese).

letteratura

• Achim Klenke: teoria della probabilità . 3a edizione. Springer-Verlag, Berlino Heidelberg 2013, ISBN 978-3-642-36017-6 , doi : 10.1007 / 978-3-642-36018-3 . 
• Christian Hesse: teoria della probabilità applicata . 1a edizione. Vieweg, Wiesbaden 2003, ISBN 3-528-03183-2 , doi : 10.1007 / 978-3-663-01244-3 .